2 Dimensional Movement

The coolest part of a quad copter is the movement. When we imagine a quad copter, we can assume the 4 rotors are always providing thrust while the machine is powered. The ability to hover in place and orient itself provides the basic functions for movement. In order to keep things simple, we will only move in 2 dimensions for now (z [forward] and y [up]). I use the following equation to implement the PD controller. (I did not implement the integral parts so it is not a traditional PID controller) The below math might look intimidating, but after being demystified, it is rather simple.

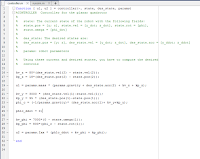
Assumptions

Since we are only operating in 2 dimensions, we make some assumptions that allows for simple calculations of motion.

1. We assume the angles used are near equilibrium. (Hover state)

2. The quad copter is small. (Agile)

U1.

The value of u1, represents the amount of thrust needed to overcome the mass of the quad copter by determining the amount of error between the current position and desired position. This can be calculated with this formula: u1 = mass * (gravity + z_ddot + kv_z + kP_z)

Variables

params.mass: The total mass of the quad copter.

params.gravity: -9.8 m/s^2.

des_state.acc(2): The double derivative of our z acceleration; also known as z_ddot. 

(Remember acceleration is the rate of change of velocity[m/s] over time so m/s^2)

The below two variables are used to "tune" the PD controller to account for the error in the system for the z axis. (over/under compensation)

kv_z: The derivative gain dampens rapidly increasing inputs. This higher the derivative gain the stronger the system reacts to error.

kp_z: The proportional gain determines the speed at which the system reacts to change. Larger inputs have a possibility to cause reactions too quickly which will make the system unstable.

U2.

The value of u2 represents the angle at which the quad copter needs to be in order to move the correct direction by determining the amount of error between the current orientation and the desired orientation. This can be calculated with this formula: u2 = Ixx * (phiC_ddot + kv_phi + kp_phi)

Variables

The below two variables are used to "tune" the PD controller to account for the error in the system for the y axis. (over/under compensation)
kv_y: The derivative gain dampens rapidly increasing inputs. This higher the derivative gain the stronger the system reacts to error.
kp_y: The proportional gain determines the speed at which the system reacts to change. Larger inputs have a possibility to cause reactions too quickly which will make the system unstable.

The below two variables are used to "tune" the PD controller to account for the error in the system for the angle of orientation. (Remember our assumptions above, this angle will be close to 0)
kv_phi: The derivative gain for the angle of orientation. The higher the value the stronger the system will react to error.
kp_phi: The proportional gain for the angle of orientation. The higher the value the quicker the system will respond to error.
phiC: PhiC is the amount of error between the current orientation and the desired orientation accounting for gravity and acceleration. This can be calculated with the following formula: (-1/gravity) * (y_ddot + kv_y + kp_y). *Note y_ddot is the 2nd derivative of y (acceleration in the y direction)
phiC_ddot: Our above assumption of small angles near equilibrium allows us to assume 0 for this value.
params.Ixx: This is the inertia of the current frame.

Tuning

Effects of increasing a parameter independently

Parameter	Rise time	Overshoot	Settling time	Steady-state error	Stability
${\displaystyle K_{p}}$	Decrease	Increase	Small change	Decrease	Degrade
${\displaystyle K_{i}}$	Decrease	Increase	Increase	Eliminate	Degrade
${\displaystyle K_{d}}$	Minor change	Decrease	Decrease	No effect in theory	Improve if ${\displaystyle K_{d}}$ small

(Source)

There are many different methods of tuning a PID controller; the most obvious being through trial and error. Using the above table, you can manually tweak the values of Kp, Ki (if implemented), and Kd in order to adjust how the quad copter reactions to over/under shoots. In my assignments for Coursera, I tuned the controller manually through trial and error but when I build a quad copter in the coming series; I will use a tuning algorithm.

Results

(Straight Line Trajectory)

(Sine Wave Trajectory)

Areas of Improvement

There are two improvements I would make to the controller. 

1. Add the integral variable to the controller. This will help with error regarding unknowns such as wind resistance or other unknown variables. 

2. We are only operating in 2 dimensions so this does not really model the real world. Adding the 3rd dimension will allow us to model real world movement and facilitate the actual building of a real quad copter.

My first post

I recently took a Quad Copter Robotics class on Coursera and I became fascinated with the whole process. Over the course, we learned how to program a PID controller and interact with a Flight Controller using Mat Lab. Now that I know how to program a quad copter I want to build one! This blog will document my journey of building and programming a real quad copter and eventually a swarm of quads that will work together to accomplish goals.

The goal of this blog is to write at least once a week about the various projects that I work on during the week. I sometimes jump around the different projects so be sure to check out the other blogs to keep up with my work! :)